Pwer ac Osgled: Watts, Volts a Decibels Cyfeiriedig

Cyflwyniad
Mewn cymwysiadau amledd radio (ond hefyd mewn llawer o gymwysiadau eraill) mae'n gyffredin iawn delio â signalau mawr iawn a bach iawn. Er enghraifft, gall transceiver drosglwyddo pŵer 100 W a derbyn dim ond 10 fW (neu 0.000'000'000'000'01 W). Gall y lefelau pŵer gwahanol iawn hyn rannu'r un cylchedau. Wrth gwrs, gellir mynegi'r ffigurau hyn yn Watts gan ddefnyddio'r nodiant peirianneg (fel uchod) neu gyda'r nodiant gwyddonol, fel 1 · 102 W a 1 · 10 - 14 W, ond maent yn eithaf anodd eu ynganu ac os yw'r esboniwr wedi'i gamsillafu , bydd y gwall o ganlyniad yn enfawr.

Ffordd arall yw cymryd y logarithm a throsi'r holl bwerau yn dBm. Mae 100 W yn dod yn + 50 dBm a 10 fW yn dod yn –110 dBm: mae'r ffigurau hyn yn llawer haws i'w trin ar y cof ac i ysgrifennu. Yna, os yw gwanhau ac ennill gwahanol flociau cylched hefyd yn cael eu mynegi yn dB, i ddod o hyd i'r pŵer terfynol, gall un ychwanegu popeth at ei gilydd yn lle lluosi, gan symleiddio cyfrifiadau ymhellach.

Nid yw pawb yn gyffyrddus ag dB, dBm ac unedau tebyg (ffug): nid oes angen llym i'w defnyddio, ond fe'u defnyddir mor eang mewn peirianneg sy'n anodd iawn eu hosgoi.

Rhywfaint o theori
Defnyddir desibelau (dB) i fynegi cymarebau pŵer mewn ffordd logarithmig, fel y gellir cymharu pwerau mawr a bach iawn gan ddefnyddio rhifau cyfforddus. Uned ffug-ddimensiwn dimensiwn yw desibel oherwydd ei fod wedi'i ddiffinio gan y gymhareb dau bŵer. Ond gan fod desibelau mor ddefnyddiol, i fynegi gwir bwer yn lle cymhareb ddimensiwn yn unig, defnyddir desibelau cyfeiriedig yn aml iawn.

Os ydym yn siarad am bŵer, mae'r hafaliad canlynol yn diffinio lefel pŵer P yn dB y pŵer p yn W y cyfeirir ato yn y pŵer p0:

Y ffactor 10 yw oherwydd bod desibelau yn "ddegfed ran y Clychau". Ond ni chlywais i erioed am unrhyw fesuriad a wnaed mewn Clychau, dim ond desibelau sy'n cael eu defnyddio.

Yr uned fwyaf cyffredin yw'r dBm (ynganu "dBm") a elwir hefyd yn dBmW neu decibel-milliwatt: dim ond y lefel pŵer yn dB yw hi o'i chymharu â phŵer cyfeirio p0 = 1 mW. Weithiau defnyddir dBW hefyd ac maen nhw'n mynegi'r gymhareb pŵer mewn perthynas â p0 = 1 W, ond nid ydyn nhw'n gyffredin iawn.

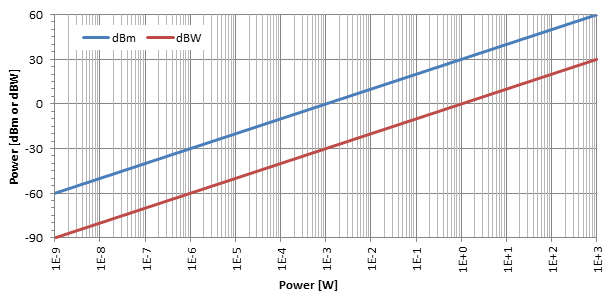
Fel y dangosir yn y plot uchod, mae effaith logarithmig y trawsnewid desibel yn eithaf amlwg. Fel y gallwch weld ar y plot leinin-log hwn, dim ond dwy linell syth yw dBm a dBW wedi'u gwahanu gan 30 dB: i drosi dBm yn dBW dim ond tynnu 30.

Mewn rhai parthau, fel derbyniad teledu analog, mae'n gyffredin mesur foltedd yn lle pŵer. Nid yw hon yn broblem cyhyd â bod y rhwystriant yn hysbys ac yn sefydlog (mae derbynyddion teledu fel arfer yn defnyddio 75 Ω).

Gall folteddau absoliwt hefyd fanteisio ar y raddfa logarithmig desibel trwy ddefnyddio decibel-microvolt (dBμV) a foltiau desibel (dBV). Y mwyaf cyffredin yw'r dBμV sy'n mynegi'r gymhareb foltedd o'i chymharu ag u0 = 1 μV. Weithiau defnyddir dBV hefyd ac maent yn mynegi'r gymhareb foltedd o'i chymharu ag u0 = 1 V.

Gwyliwch fod folteddau'n defnyddio "20" yn lle "10" yn eu fformiwla dB. Mae hyn oherwydd bod desibelau bob amser yn cael eu diffinio fel dognau pŵer; os mai folteddau yn unig sydd gennym, mae'n rhaid i ni eu sgwario yn gyntaf i ddod o hyd i'r pŵer. Bydd y pŵer hwnnw o ddau, o'i dynnu allan o'r logarithm, yn lluosi ffactor presennol 10 â 2.

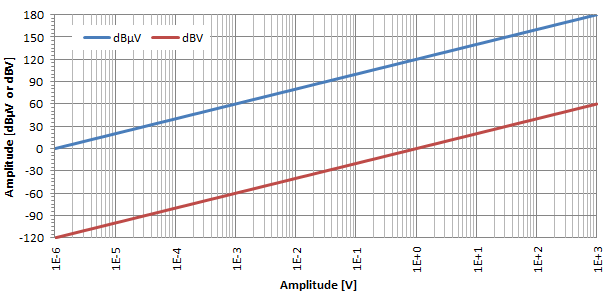
Fel y dangosir yn y plot uchod ac mewn ffordd debyg ag o'r blaen, mae effaith logarithmig y trawsnewid desibel yn eithaf amlwg hefyd ar gyfer folteddau. Fel y gallwch weld ar y plot log-lin hwn, dim ond dwy linell syth yw dBμV a dBV wedi'u gwahanu gan 120 dB: i drosi dBμV yn dBV, tynnwch 120 yn unig.

Nawr, os ydym am drosi o bŵer i foltedd ac i'r gwrthwyneb, mae angen i ni wybod y rhwystriant. Rydym yn defnyddio'r hafaliad canlynol yn unig:

Mae'r trosiad hwn yn ddilys dim ond pan fydd y rhwystriant Zc yn real a bod y llwyth wedi'i gyfateb i'r llinell drosglwyddo.

Os ydym yn plotio'r lefel pŵer mewn dBm a'r lefel osgled yn dBμV fel swyddogaeth pŵer yn W am rwystriant penodol (yma Zc = 50 Ω) rydym yn cael y canlynol:

Fel o'r blaen, mae gennym ddwy linell gyfochrog 107 dB ar wahân. Felly, i drosi o dBm i dBμV, dim ond ychwanegu 107 dB ar gyfer Zc = 50 Ω, ychwanegu 109 dB ar gyfer Zc = 75 Ω, ychwanegu 115 dB ar gyfer Zc = 300 Ω neu ychwanegu 118 dB ar gyfer Zc = 600 Ω.

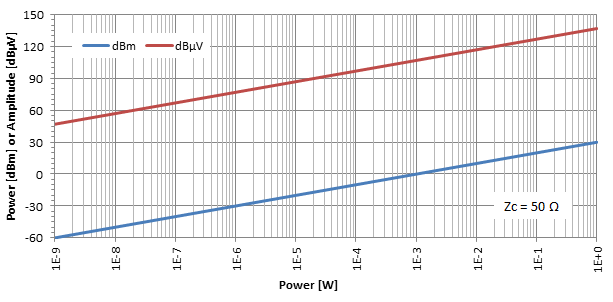
Ystyriaethau ymarferol
Ar yr olwg gyntaf, efallai y bydd rhywun yn meddwl, oherwydd y logarithm, bod cyfrifiannell poced yn gwbl angenrheidiol i ddelio â dBm. Mewn gwirionedd, mae'n hawdd gwneud cyfrifiad bras yn eich pen. Mae'n rhaid i chi gofio dim ond tair ffaith:
 Pwer o 1 mW yw 0 dBm.
 Bob tro mae'r pŵer yn dyblu, ychwanegwch 3 dB.
 Bob tro mae'r pŵer yn cynyddu gan ffactor o 10, ychwanegwch 10 dB.

Nawr, gadewch i ni ystyried ychydig o enghreifftiau: mae'n debyg bod gennym ni lefel pŵer o 26 dBm. Gallwn ysgrifennu 26 dBm = 0 dBm + 10 dB + 10 dB + 3 dB + 3 dB, a chyda'r tair rheol flaenorol syml, gallwn ddod o hyd i'r pŵer yn hawdd trwy wneud 1 mW · 10 · 10 · 2 · 2 = 400 mW .

Enghraifft arall: mae'n debyg bod gennym –33dBm: gallwn ysgrifennu fel –33 dBm = 0 dBm - 10 dB - 10 dB - 10dB - 3 dB, ac rydym yn dod o hyd i 1 mW / 10 / 10 / 10 / 2 = 0.5 μW.

Mae hyn hefyd yn gweithio mewn ffordd arall, er enghraifft dim ond 50 mW · 1 · 10 / 10 yw 2 mW. Mewn dBm mae gennym 0 dBm + 10 dB + 10 dB –3 dB = 17 dBm.

Mae hyn yn gofyn am rywfaint o ymarfer ond mae'n hawdd iawn ei wneud. Nid yw mor gywir â chyfrifiannell poced oherwydd dim ond ar ± 2 dB y gallwch chi fod yn gywir ond, am yr ymdrech, mae'n rhoi syniad da iawn o gryfder signal.

Mae dull tebyg hefyd yn gweithio ar gyfer dBμV, ond mae'r rheolau yn wahanol:
 Osgled o 1 μV yw 0 dBμV.
 Bob tro mae'r osgled yn dyblu, ychwanegwch 6 dB.
 Bob tro mae'r osgled yn cynyddu gan ffactor o 10, ychwanegwch 20 dB.

Efallai y byddwch chi'n synnu am y cyfrifiadau mewn desibelau a ddangoswyd o'r blaen, lle mae dB yn cael ei ychwanegu at dBm, sy'n eithaf rhyfedd. Mae hyn oherwydd bod desibelau yn unedau ffug ac nad ydyn nhw'n ymddwyn fel arfer. Mynegir cymhareb dau bŵer yn dB ond mae'n ddimensiwn: er enghraifft dim ond "dwywaith cymaint" y mae 3 dB yn ei olygu. Mae'r pŵer a fynegir yn dBm yn bwer mewn gwirionedd: er enghraifft mae 10 dBm yn golygu "mae 10 gwaith yn gryfach na 1 mW", sef 10 mW.

Nawr, pan fyddwch chi'n ychwanegu desibelau (dB, dBm, ...), oherwydd eu natur logarithmig, rydych chi mewn gwirionedd yn lluosi'r ffigurau gwreiddiol gyda'i gilydd. Felly, os ydych chi'n ychwanegu enillion o 3 dB i bŵer 10 dBm, rydych chi'n cael 13 dBm. Ond yr hyn a wnaethoch mewn gwirionedd, yw lluosi ffactor o 2 â phŵer 10 mW yn sicrhau 20 mW, sef 13 dBm!

Hyd yn hyn cystal, mae ychwanegu yn llawer haws i'w wneud yn eich pen na lluosi, ac mae hyn yn gwneud desibelau mor ddefnyddiol. Ond mae problem: gan fod ychwanegu desibelau at ei gilydd yn cyfateb i luosi'r ffactorau gwreiddiol, sut y gall un ychwanegu (cyfuno) pŵer dau signal? Wel, allwch chi ddim. Ni allwch ychwanegu dBm at dBm. Er enghraifft, os oes gennych gylched neu ddyfais sy'n cyfuno pŵer un signal o 10 dBm (10 mW) â phwer signal arall o 13 dBm (20 mW), y canlyniad yw 10 mW + 20 mW = 30 mW sef 14.8 dBm. Nid oes unrhyw ffordd o wneud hyn yn uniongyrchol mewn dBm, mae'n rhaid i chi drosi'r ddau bŵer yn Watts, eu hychwanegu at ei gilydd a'u trosi yn ôl yn dBm. Mae hwn yn gyfyngiad mawr ar desibelau a chwymp cyffredin; yn ffodus nid yw'r llawdriniaeth hon yn gyffredin iawn.

Os hoffech chi adeiladu gorsaf radio, rhoi hwb i'ch trosglwyddydd radio FM neu angen unrhyw un arall Offer FM, mae croeso i chi gysylltu â ni: [e-bost wedi'i warchod].

Gadewch neges 

Rhestr negeseuon