Tiwtorial Decibel: dB a dBm yn erbyn Ennill a Milliwatts

Mae'r cysyniad o desibel (dB) yn ddealladwy anodd ac yn ddryslyd i rywun sydd newydd gael ei gyflwyno iddo. Mae cyfuno manylebau ar gyfer ennill, pŵer, a foltedd (a cherrynt, ond nid mor aml) sy'n cymysgu dB, dBm, dBW, watiau, miliwatiau, foltedd, milivolts, ac ati, yn aml yn gofyn am drosi yn ôl ac ymlaen rhwng gwerthoedd llinellol a gwerthoedd desibel. Bydd y tiwtorial byr hwn yn helpu i egluro'r gwahaniaeth rhwng gweithio gyda desibelau a gweithio gyda gwerthoedd llinol.

Cafodd logarithmau (boncyffion) eu cenhedlu gyntaf yn gynnar yn yr 1600s gan fathemategydd yr Alban John Napier, fel offeryn ar gyfer symleiddio gweithrediadau lluosi a rhannu trwy eu trosi i weithrediadau adio a thynnu cyflymach a llai tueddol o gamgymeriad, yn y drefn honno. Gwneir hyn yn bosibl oherwydd y ffordd y gellir lluosi dau rif a fynegir fel rhifau sylfaen tebyg ag esbonwyr trwy ychwanegu'r esbonwyr at ei gilydd yn unig. Cyflawnir rhaniad o'r un niferoedd hynny trwy dynnu'r esbonwyr. Mae'n un o ddeddfau esbonwyr, ac mae'n edrych fel hyn:

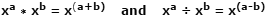
Gan ddefnyddio rhifau gwirioneddol fel enghraifft, lle mae x = 10, a = 4, b = 1:

Mae cyfraith esbonwyr yn gweithio ar gyfer unrhyw rif sylfaen, nid 10 yn unig. I ffraethineb:

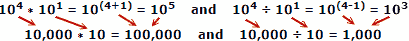
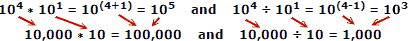
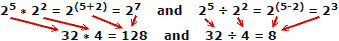
Mae pobl yn tueddu i wneud llai o gamgymeriadau wrth adio a thynnu rhifau, felly mae mantais logarithmau yn amlwg. Cofiwch fod logarithmau wedi'u datblygu cyn bod cyfrifiaduron mecanyddol neu electronig awtomatig ar gael. Mae rheol sleidiau yn manteisio ar briodweddau logarithmau i'w cyfrifo, ond mae hwnnw'n bwnc o bwys ar wahân.

Mae'r rheini'n enghreifftiau syml, ond yn dal unrhyw sylfaen neu esboniwr. Yn absenoldeb cyfrifiannell, er mwyn bod yn ddefnyddiol ar gyfer cymhwysiad cyffredinol mae angen tabl rhifau a'u logarithmau cyfatebol. Roedd tablau log cynnar yn llenwi cyfeintiau, yn dibynnu ar y bylchau rhwng rhifau (1.000, 1.001, 1.002, 1.003, vs. 1.0, 1.1, 1.2, 1.3, ac ati). Y newyddion da i grewyr tablau logarithm yw mai dim ond un 'degawd' o rifau (ee, 1 trwy 10) sy'n ofynnol gan fod pob degawd blaenorol neu seceding yn lluosrif syml o bŵer 10.

Nodyn: Rwy'n defnyddio sylfaen 10 yn y drafodaeth hon gan mai dyna yw sylfaen ein system rhifau cyffredin - a dyna pam mae'r term 'logarithm cyffredin' ar gyfer logiau 10 sylfaen. Efallai eich bod wedi clywed am logarithmau naturiol, sy'n defnyddio sylfaen e, ond ni chaiff e ei ddefnyddio'n aml iawn wrth gyfrifo pŵer trydanol graddfa, foltedd a meintiau cyfredol (er ei fod yn cael ei ddefnyddio pan fydd onglau cyfnod yn cael eu cynnwys, hy hunaniaeth Euler). Ysgrifennir logarithmau naturiol fel ln (x) heb yr is-danysgrifiad 'e', ​​ond fel rheol ysgrifennir logarithmau 10 sylfaen yn syml fel log (x) heb y tanysgrifiad 10; hy, nid loge (x) na log10 (x), yn y drefn honno.

Fesul sylfaen = Tabl log 10:

Papur Graff Peirianneg Beiciau Lled-Logarithmig 5 - Caffi RF Yr eithriad a'r achos arbennig yw logx (0) = Heb ei ddiffinio. Mae hynny felly oherwydd nad oes unrhyw bŵer y gallwch chi godi unrhyw rif iddo a chael 0 (sero). Gallwch fynd at sero yn anghymesur, ond ni allwch gyrraedd sero. Ni fydd byth y rhif sero yn cael ei arddangos ar raddfa log; maent fel arfer yn rhedeg o ryw bŵer 10 i ryw bŵer arall o ddeg. Dangosir enghraifft o bapur graff log ar y dde. Mae ganddo 'gylchoedd' neu 'ddegawdau' 5 o ystod. Sylwch nad oes sero ar yr echelin-y.

Logarithm sylfaen-10 (cyffredin) rhif, felly, yw'r esboniwr y mae'n rhaid codi 10 iddo er mwyn cael y rhif hwnnw. Mewn geiriau eraill, gan fod 10 a godwyd i bŵer 2 yn hafal i 100 (102 = 100), log sylfaen-10 100 yw 2 (log10 100 = 2).

Dyma gyfraith sylfaenol logarithmau:


Perfformio'r un lluosiadau a rhaniadau ag a wneir ar frig y dudalen trwy ddefnyddio logarithmau go iawn:



Mae hynny'n iawn, ond yr hyn rydych chi'n ei wneud yn y pen draw yw logarithm y rhif rydych chi'n ei geisio. Cwestiwn: Ac eithrio enghraifft syml fel hon, sut ydych chi'n cael yr ateb sydd ei angen arnoch chi? Ateb: Chwiliwch am antilogarithm (antilog) y canlyniad. Yn yr achos hwn:

Efallai y bydd enghraifft anoddach, a mwy tebygol gyda rhifau nad ydynt yn bwerau cyfanrif 10, yn edrych yn debyg i'r canlynol:




 Cyfrifiannell HP-35 (wikipedia) - RF CafeSince mae logarithm 'x' yn hafal i 1.8444, mae'r antilog yn hafal i 'x,' sef 69.9



Defnyddiais fy nghyfrifiannell i edrych i fyny'r logiau a'r antilogs ar gyfer y niferoedd hynny, ond cyn 1972 pan gyflwynodd Hewlett Packard (HP) eu cyfrifiannell wyddonol HP-35, roedd angen i'r person cyffredin heb fynediad at gyfrifiadur prif ffrâm corfforaethol neu brifysgol ddefnyddio log tabl i berfformio cyfrifiadau o'r fath.

Pwy sy'n trafferthu defnyddio logarithmau heddiw, efallai y byddwch chi'n gofyn? Llawer o bobl, gan gynnwys fi, yn eithaf aml wrth gyfrifo paramedrau system raeadredig fel ffigur sŵn (NF) a phwyntiau rhyngdoriad (IP). Nid yw adio a thynnu gwerthoedd dB a phŵer dBm syml yn gweithio gyda NF ac IP. Mae'r fformwlâu llywodraethu yn defnyddio lluosi a rhannu gwerthoedd ennill llinellol a phwer, sy'n gofyn am drosi dB a / neu dBm yn gyntaf i rifau llinol (cymhareb ennill a mW) gan ddefnyddio antilogs, cyflawni'r cyfrifiadau rhaeadru, ac yna trosi'r canlyniad yn ôl i dB a / neu dBm gan ddefnyddio logiau.

Nid oes angen trosi holl weithrediadau rhaeadru'r system yn ôl ac ymlaen. Er enghraifft, os mai dim ond cyfanswm ennill y system a / neu lefel pŵer allbwn sydd ei angen, yna gellir gwneud cyfrifiadau gydag naill ai unedau llinol (mW a lluosyddion) neu unedau logarithmig (dBm a dB, yn y drefn honno).

Y Diffiniad o 'dB' a 'dBm'

Diffinnir desibel (dB) mewn peirianneg drydanol fel 10 yn fwy na logarithm sylfaen-10 cymhareb rhwng dwy lefel pŵer; ee, Pout / Pin (ennill, mewn geiriau eraill). I ffraethineb:

Felly, mynegir pob enillion sy'n fwy nag 1 fel desibelau positif (> 0), a mynegir enillion o lai nag 1 fel desibelau negyddol (<0). Sylwch, ar gyfer achosion y mae'r rhan fwyaf ohonom yn dod ar eu traws, rhaid i'r gymhareb linellol o P1 / P2 fod yn rhif positif (> 0) gan fod logarithm 0 heb ei ddiffinio a bod logarithm rhifau negatif yn gymhleth (maent yn cynnwys rhan real a dychmygol. ). Gall y gwerth dB, serch hynny, gymryd unrhyw werth rhwng −∞ a + ∞, gan gynnwys 0, sy'n ennill 1 [10 * log (1) = 0 dB].

Mae 'dBm' yn uned pŵer wedi'i seilio ar desibel y cyfeirir ati at 1 mW. Gan fod 0 dB o ennill yn hafal i ennill 1, mae 1 mW o bŵer yn 0 dB yn fwy na 1 mW, neu 0 dBm. Yn yr un modd, mae uned bŵer dBW yn desibelau mewn perthynas â 1 W o bŵer.


Yn unol â hynny, mae'r holl werthoedd dBm sy'n fwy na 0 yn fwy na 1 mW, ac mae'r holl werthoedd dBm sy'n llai na 0 yn llai na 1 mW (gweler Ffig. 1). Er enghraifft, mae + 3.01 dBm yn 3.01 dB yn fwy na 1 mW; hy, neu 0 dBm + 3.01 dB = + 3.01 dBm (2 mW). Mae −3.01 dBm yn 3.01 dB yn llai na 1 mW; hy, neu 0 dBm + (−3.01) dB = −3.01 dBm (0.5 mW).

Mae'r tabl canlynol yn rhoi rhai enghreifftiau rhifiadol fel y gallwch weld y gydberthynas rhwng mW a dBm. Byddai'r un set o werthoedd wedi'u plotio ar raddfa logarithmig yn cynhyrchu llinell syth. Oherwydd y berthynas logarithmig, mae'r graff yn baglu'r gwerthoedd llai yn erbyn yr echelin fertigol chwith. Mae fersiwn chwyddedig o'r rhanbarth 0 i 1 mW wedi'i mewnosod er eglurder.

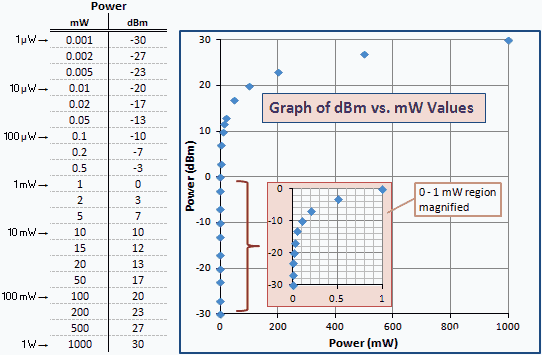
Ffig. 1 - Graff Pwer mewn Unedau dBm vs mW

Tabl a graff o gymarebau enillion llinellol dB yn debyg i'r dBm vs mW yn Ffig. 2 yw Ffig. 1. Sylwch fod y niferoedd a'r cromliniau yn union yr un peth; dim ond y labeli echelin sy'n cael eu newid. Mae hynny oherwydd bod dBm yn uned pŵer a fynegir yn dB o'i gymharu â 1 mW (0 dBm).

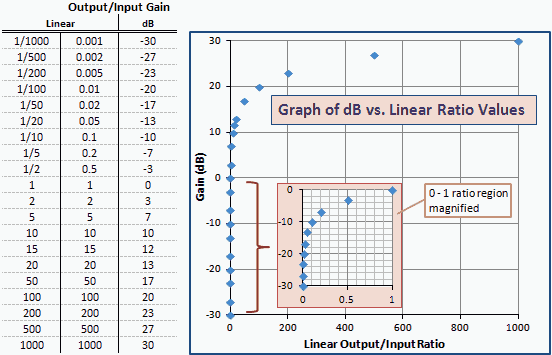
Ffig. 2 - Graff Ennill mewn Unedau Cymhareb Llinol dBm vs.

Yn sylfaenol, ffactor lluosi (neu rannu) yw ennill. Er enghraifft, gallai mwyhadur gael enillion sy'n cynyddu'r signal gan ffactor o 4 (hy, 4x) o fewnbwn i allbwn (gweler Ffig. 3). Os yw signal 1 mW (0 dBm) yn cael ei fwydo i'r mwyhadur, yna daw 1 mW * 4 = 4 mW allan. O ran desibelau, mae ffactor o 4 yn cyfateb i log 10 * (4) = 6.02 dB, felly mae 0 dBm yn ogystal â 6.02 dB o enillion yn cynhyrchu + 6.02 dBm ar yr allbwn.

1 mW * 4 = 4 mW

0 dBm + 6.02 dB = 6.02 dBm

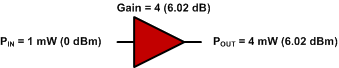
Ffig. 3 - Ennill mwyhadur sengl.

Cyfuno Enillion (llinol a dB) w / Gwerth Cadarnhaol

Os yw mwyhadur ag ennill 4 mewn cyfres ag ail fwyhadur gydag enillion o 6, yna cyfanswm yr ennill yw 4 * 6 = 24. O ran desibelau, mae ffactor o 6 yn cyfateb i log 10 * (6) = 7.78 dB, ac mae ffactor o 24 yn cyfateb i log 10 * (24) = 13.8 dB.

Yn union fel 4 x 6 = 24 (ennill llinol), 6.02 dB + 7.78 dB = 13.8 dB (ennill desibel).

Os yw signal 1 mW (0 dBm) yn cael ei fwydo i'r mwyhadur, yna daw 4 mW allan o'r mwyhadur cyntaf, a daw 24 mW allan o'r ail fwyhadur. Gweler Ffig. 4.

1 mW * 4 * 6 = 24 mW
0 dBm + 6.02 dB + 7.78 dB = 13.8 dBm

Ffig. 4 - Ennill mwyhadur deuol rhaeadredig.

Cyfuno Ennill a Cholled (llinol a dB)
Mae'r enghraifft nesaf hon yn dangos beth sy'n digwydd pan ddaw enillion <1 (colled) ar draws, lle mae attenuator ag ennill 1/6 yn cael ei osod ar ôl y mwyhadur cyntaf yn lle cael ail fwyhadur. Gweler Ffig. 5.
4 * 1 / 6 = 2 / 3 (ennill llinol). Yn yr un modd 6.02 dB - 7.78 dB = −1.76 dB (ennill desibel).
Yn yr un modd â'r enghraifft flaenorol, os yw signal 1 mW (0 dBm) yn cael ei fwydo i'r mwyhadur gydag enillion o 4, yna daw 4 mW allan. Yna mae'r 4 mW hwnnw'n mynd i mewn i'r attenuator gydag enillion llinellol o 1 / 6 ac yn dod allan ar lefel pŵer o 4 / 6 mW (2 / 3 mW).
Cyfanswm yr ennill yn yr achos hwn yw 4 / 6 = 2 / 3, felly bydd y pŵer allbwn mewn gwirionedd yn llai na'r pŵer mewnbwn.

1 mW * 4 * 1 / 6 = 2 / 3 mW = 0.67 mW

0 dBm + 6.02 dB + (-7.78 dB) = −1.76 DBM

Ffig. 5 - Ennill mwyhadur rhaeadru ac attenuator.

12 mW + 34 mW + 8 mW + 20 dB

Gwybodaeth Atodol ar Logarithmau
Logarithmau Cynhyrchion
Mae eiddo o logarithmau a ddefnyddir yn ymhlyg uchod yn nodi'r canlynol, ac mae'n sail ar gyfer gallu ychwanegu a thynnu gwerthoedd logarithm yn lle lluosi eu cyfwerthoedd llinol.

gallai 'h * j / k * m / n' gynrychioli rhaeadr o gydrannau sydd â thair dyfais (h, j, a m) pob un ag ennill> 1 a dwy ddyfais (k ac n) pob un ag ennill <1 (gweler Ffig. 6). Gellir cyfrifo cyfanswm enillion y system naill ai trwy luosi'r holl werthoedd ennill llinellol gyda'i gilydd neu ychwanegu'r holl werthoedd enillion desibel gyda'i gilydd.

Ffig. 6 - Cydrannau rhaeadru

Logarithmau Esbonwyr
Mae'r canlynol yn bwysig er mwyn deall pam mae ennill pŵer o ran pŵer yn 10 * log (Pout / Pin) dB, tra bod enillion pŵer o ran foltedd yn 20 * log (Vout / Vin) dB.


mae hyn oherwydd bod cf yn hafal i c wedi'i luosi ag amseroedd 'f' ei hun. Er enghraifft, os yw f = 4:


Ennill Pwer Yn Seiliedig ar Ennill Pwer yn erbyn Pwer Yn Seiliedig ar Foltedd
Ennill pŵer yw Pout / Pin, ac enillion foltedd yw Vout / Vin. Diffinnir enillion pŵer yn seiliedig ar gymhareb pŵer mewn desibelau fel log 10 * (Pout / Pin). Ennill pŵer o ran foltedd, yw [(Vout2 / R) / (Vin2 / R)], ers yn ôl deddf Ohm P = V2 / R. Mae'r 'R' yn yr enwaduron yn canslo gan adael Vout2 / Vin2, sy'n hafal i (Vout / Vin) 2, fel y'i diffinnir gan reol yr esbonwyr sy'n dweud ac / bc = (a / b) c. Felly:

Nodyn Pwysig: Enillion foltedd o ran foltedd yw log 10 * (Vout / Vin) dB, yr un fath ag enillion pŵer o ran pŵer. Dim ond pan fynegir enillion pŵer yn nhermau foltedd y mae hafaliad log 20 * (Vout / Vin) dB yn berthnasol. Mae hwn yn bwynt cyffredin o ddryswch.


Nid oes unrhyw weithrediad mewn mathemateg yn fympwyol, ac mae hynny'n mynd am pam mae colled pŵer signal (ennill <1) yn cael ei bortreadu fel gwerth negyddol, ac felly'n cael ei dynnu yn ystod cyfrifiad rhaeadru. Mae'n arddangosiad syml, ond yn werth ei grybwyll.

log (1 / f) = log (1) - log (f) = 0 - log (f) = -log (f)

Os hoffech chi adeiladu gorsaf radio, rhoi hwb i'ch trosglwyddydd radio FM neu angen unrhyw un arall Offer FM, mae croeso i chi gysylltu â ni: [e-bost wedi'i warchod].

Gadewch neges 

Rhestr negeseuon